Пи полином ли е?

Видео: Пи полином ли е?

2024 Автор: Lynn Donovan | [email protected]. Последно модифициран: 2023-12-15 23:43

Пи (π) не се счита за a полином . Това е стойност, отнасяща се до обиколката на кръг. От друга страна, полином се отнася до уравнение, съдържащо четири или повече променливи.

Тук може ли pi да бъде част от полином?

Отговорът е НЕ. Ако имаше a полином с алгебрични коефициенти ще има и a полином с рационален коефициент (с по-голяма степен). Това е така, защото ˉQ е алгебрично затворен. Предполага че π бяха коренът на a полином f(x)=xn+an−1xn−1+⋯+a0, като ai са алгебрични числа.

Второ, какво прави полином? В математиката, а полином е израз, състоящ се от променливи (наричани още неопределени) и коефициенти, който включва само операциите събиране, изваждане, умножение и неотрицателни цели степени на променливи. Пример за а полином на единичен неопределен, x е x² − 4x + 7.

В това отношение, Пи мононом ли е?

Да, π π е a едночленен защото е число.

Трябва ли полиномът да има променлива?

Така че: А полином мога имат константи, променливи и степени, но никога деление на a променлива . Те също могат имат един или повече термини, но не безкраен брой термини.

Препоръчано:

Как се нарича полином с 6 члена?

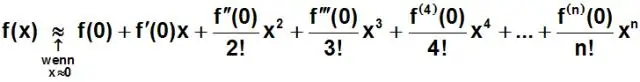
Следните имена се приписват на полиноми според степента им: Степен 4 – квартичен (или, ако всички термини имат четна степен, биквадратичен) Степен 5 – квинт. Степен 6 - секстичен (или, по-рядко, хексичен)

Какво е полином от първа степен?

Полиноми от първа степен. Полиномите от първа степен са известни още като линейни полиноми. По-специално, полиноми от първа степен са линии, които не са нито хоризонтални, нито вертикални. По-често буквата m се използва като коефициент на x вместо a и се използва за представяне на наклона на линията