Съдържание:
Видео: Как решавате уравнения в Mathcad?
2024 Автор: Lynn Donovan | [email protected]. Последно модифициран: 2023-12-15 23:43
Да се Решаване на уравнения Символично. Въведете уравнение да се реши използвайки оператора Boolean равно на. Поставете символния оператор за оценка, въведете ключовата дума реши в заместителя и след това натиснете Enter или щракнете където и да е. PTC Mathcad връща символични решения на уравнение , ако е възможно.
Освен това, как използвате функцията root в Mathcad?
За намиране на комплекс корен , трябва да започнете със сложна стойност за първоначалното предположение. Използвайки парцел и коренна функция да намеря корени на израз. Mathcad оценява на root функция с помощта методът на секанта. Предполагаемата стойност, която предоставяте за x, става отправна точка за последователни приближения на корен стойност.
Също така, как решавате система от уравнения в Matlab? Решаване на системата на линейни Уравнения Използване на linsolve Помислете за следното система . Декларирайте система от уравнения . syms x y z eqn1 = 2*x + y + z == 2; eqn2 = -x + y - z == 3; eqn3 = x + 2*y + 3*z == -10; Използвайте equationsToMatrix, за да преобразувате уравнения във формата AX = B.
Също така да знаете как решавате уравнения?
Ето някои неща, които можем да направим:
- Добавете или извадете една и съща стойност от двете страни.
- Изчистете всички дроби, като умножите всеки член по долните части.
- Разделете всеки член на една и съща стойност, различна от нула.
- Комбинирайте Условия за харесване.
- Факторинг.
- Разширяването (противоположното на факторинга) също може да помогне.
Какво означава Z в Matlab?
Отговори (1) MATLAB го прави това автоматично в този случай. Но за да отговоря на въпроса ви, root(f( z ), z ) означава набор от стойности, z , така че f( z ) == 0 -- корените на f( z ). В частност направи не разчитайте, че първият корен е реално оценен (ако някой от корените е) или положителен (ако някой от тях е дори положителен).
Препоръчано:
Как Таритаун получи името си Как Sleepy Hollow получи името си?
Как Sleepy Hollow получи името си? Името Таритаун е дадено от домакините на съседната страна, защото съпрузите чакат около селската механа в пазарни дни. Името Sleepy Hollow идва от сънливото мечтателно влияние, което сякаш надвисва над земята
Как да намеря IDoc грешки и как да ги обработвате отново?
След проверка на грешката в транзакцията BD87 и основната причина, трябва да е възможно повторното обработване на IDoc, като се следват стъпките по-долу: Отидете на WE19, изберете IDoc и изпълнете. Ще бъдат показани подробности за IDoc. Променете данните в сегмента според вашето изискване. Кликнете върху стандартния входящ процес
Как решавате организационен параграф?
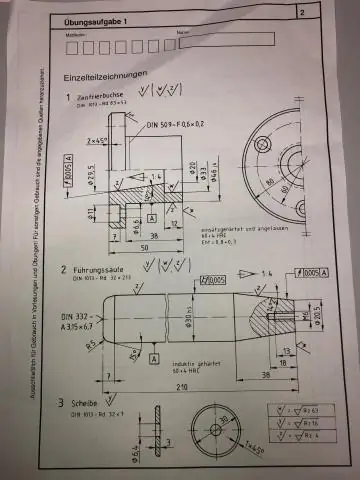
ВИДЕО По същия начин, как отговаряте на параграф за организация? (Английски) Прочетете всички изречения, докато се опитвате да намерите изречението по темата. Вземете решение за второ изречение, като организирате идеите логически чрез улики в контекста и конструкцията на изречението.
Как се създава масив в Mathcad?
Масив в Mathcad може да бъде създаден по следните няколко начина: Въведете команда Insert, Martrix; Натиснете комбинацията Ctrl + M; Кликнете върху бутона „Вектор или матрица“на лентата с инструменти „Матрица“
Защо тригонометричните идентичности са полезни при решаването на уравнения?
Идентичностите ни позволяват да опростяваме сложни изрази. Те са основните инструменти на тригонометрията, използвани при решаването на тригонометрични уравнения, точно както разлагането на множители, намирането на общи знаменатели и използването на специални формули са основните инструменти за решаване на алгебрични уравнения