Видео: Включвате ли извънредни стойности в обобщението на 5 числа?
2024 Автор: Lynn Donovan | [email protected]. Последно модифициран: 2023-12-15 23:43
В пет числа са минималната, стойността на първия квартил (Q1), медианата, стойността на третия квартил (Q3) и максималната. Първото нещо Вие може да забележите за този набор от данни е номер 27. Това е много различно от останалите данни. Това е извънредно и трябва да бъде премахнат.
Тук включвате ли извънредни стойности в диапазона?
Обхват е доста полезна индикация за това колко са разпределени данните, но има някои сериозни ограничения. Това е така, защото понякога данните могат да имат отклонения които са значително извън другите точки от данни. В тези случаи, обхват може да не даде вярна индикация за разпространението на данни.
какво се счита за извънредно? Ан извънредно е наблюдение, което се намира извън цялостния модел на разпределение (Moore and McCabe 1999). Удобна дефиниция на an извънредно е точка, която пада повече от 1,5 пъти от интерквартилния диапазон над третия квартил или под първия квартил.
По този начин от какво се състои обобщението с 5 числа?
пет- номера обобщения А пет - резюме на номера е особено полезен при описателни анализи или по време на предварителното изследване на голям набор от данни. А резюмето се състои от пет стойности: най-екстремните стойности в набора от данни (максималните и минималните стойности), долния и горния квартил и медианата.
Какво е правилото 1.5 IQR?
Използване на Interquartile Правило за намиране на отклонения Умножете интерквартилния диапазон ( IQR ) от 1.5 (константа, използвана за разпознаване на отклонения). Добавете 1.5 х ( IQR ) до третия квартил. Всяко число, по-голямо от това, е предполагаемо отклонение. Извадете 1.5 х ( IQR ) от първия квартил. Всяко число по-малко от това е предполагаемо отклонение.
Препоръчано:
Какво представлява грешката в обобщението в машинното обучение?
В приложенията за контролирано обучение в машинното обучение и теорията на статистическото обучение грешката в обобщаването (известна още като грешка извън извадката) е мярка за това колко точно алгоритъмът е в състояние да предвиди стойности на резултатите за невиждани преди данни
Функцията count брои ли нулеви стойности?
Пример - Функцията COUNT включва само стойности NOT NULL Не всеки осъзнава това, но функцията COUNT ще брои само записите, където изразът НЕ е NULL в COUNT(израз). Когато изразът е стойност NULL, той не се включва в изчисленията COUNT
Как автоматично да копирам и поставям стойности в Excel?
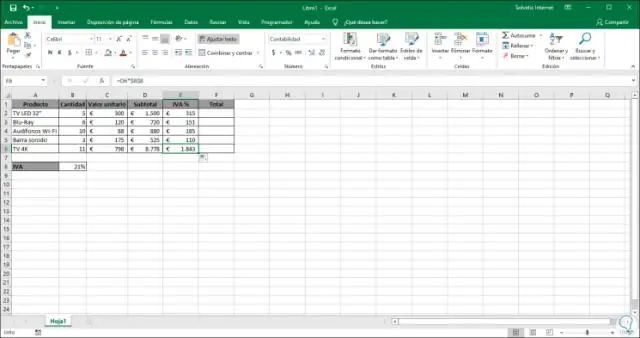
Поставяне на стойности, а не на формули В работен лист изберете клетките, които съдържат резултантната стойност на формула, която искате да копирате. В раздела Начало, в групата Клипборд щракнете върху Копиране или натиснете CTRL+C на клавиатурата си. Изберете горната лява клетка на областта за поставяне. В раздела Начало, в групата Клипборд щракнете върху Поставяне и след това върху Поставяне на стойности
Как да премахна липсващите стойности в R?
Първо, ако искаме да изключим липсващи стойности от математически операции, използвайте na. rm = TRUE аргумент. Ако не изключите тези стойности, повечето функции ще върнат NA. Може също да желаем да поднаборим нашите данни, за да получим пълни наблюдения, тези наблюдения (редове) в нашите данни, които не съдържат липсващи данни
Включвате ли извънредни стойности в стандартното отклонение?
Стандартното отклонение никога не е отрицателно. Стандартното отклонение е чувствително към отклонения. Единичен отклонение може да повиши стандартното отклонение и от своя страна да изкриви картината на разпространението. За данни с приблизително еднакво средно значение, колкото по-голям е спредът, толкова по-голямо е стандартното отклонение