Видео: Диагоналите на квадратен ъгъл са ъглополовящи?
2024 Автор: Lynn Donovan | [email protected]. Последно модифициран: 2023-12-15 23:43
В квадрат има следните свойства:
Прилагат се всички свойства на ромб (тези, които имат значение тук са успоредните страни, диагонали са перпендикулярни бисектриси един от друг и диагонали разполовява ъгли ). Всички свойства на правоъгълника се прилагат (единственото, което има значение тук е диагонали са конгруэнтни).
Тук диагоналите на правоъгълен ъгъл ъглополовящи ли са?
В диагонали на правоъгълник ще разполовява само ъгли ако страните, които се срещат при ъгъл са равни: с други думи, само ако правоъгълник е квадрат. Друг начин да се мисли за това: ъгъл е право- ъгъл , и на бисектриса на ъгъла трябва да излезе на половината вдясно - ъгъл към страните. Оттук и правоъгълник трябва да е квадратна.
Може също да се запитаме дали диагоналът на квадрата се разделя? А квадрат е специален случай на равнобедрен трапец, хвърчило, паралелограм, четириъгълник, правоъгълник, ромб и трапец. В диагонали на а квадратно разполовяване един друг и са перпендикулярни (илюстрирани в червено на фигурата по-горе). Освен това те разполовява всеки двойка противоположни ъгли (илюстрирани в синьо).
Имайки предвид това, в кои четириъгълници диагоналите делят ъглите?
А четириъгълник е ромб, ако: това е успоредник и двойка съседни страни са равно, си диагоналите разполовяват един друг вдясно ъгли , си диагоналите разполовяват всеки връх ъгъл.
Какъв е диагоналът на квадрата?
Диагонали на а квадрат . А квадрат има две диагонали , които са отсечки, свързващи противоположни върхове (ъгли) на квадрат . С други думи, точката, в която диагонали пресичат (кръстосват), разделя всеки диагонал на две равни части. Всеки диагонал разделя на квадрат на два равни равнобедрени правоъгълни триъгълника.
Препоръчано:
Какви са иконите с малка стрелка в долния ляв ъгъл?
Малката стрелка в долния ляв ъгъл на иконата показва, че иконата е икона за пряк път. Иконите за пряк път са за стартиране на програмата, която представлява
Равни ли са диагоналите на квадрата?
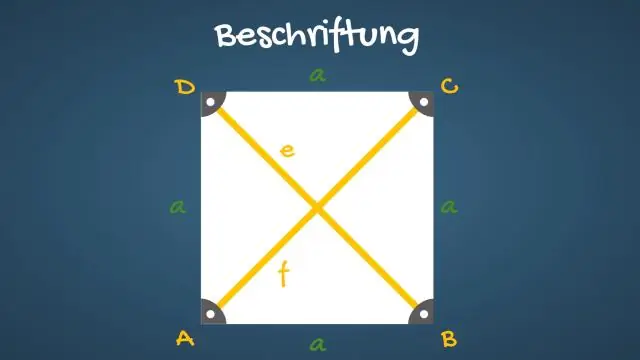
Диагоналите на квадрата разполовяват ъглите му. Противоположните страни на квадрата са успоредни и равни по дължина. И четирите страни на квадрата са равни. Диагоналите на квадрата са равни
Каква е точката на паралелност за сисектриса на ъгъл?
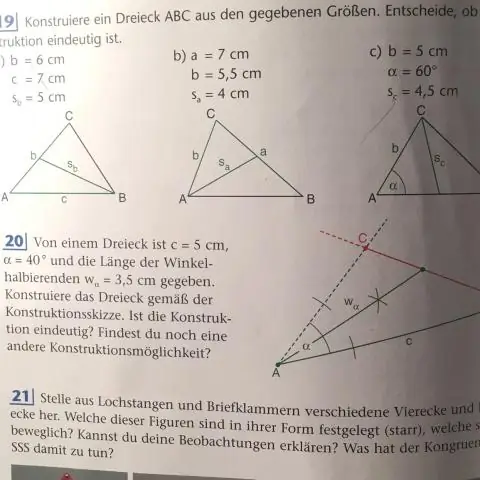
Точката на паралелност на симетралите на ъгъла се нарича инцентър. Трите височини на триъгълника са едновременни. Точката на паралелност се нарича ортоцентър. Трите медиани на триъгълника са едновременни
Винаги ли диагоналите се разделят помежду си в паралелограм?
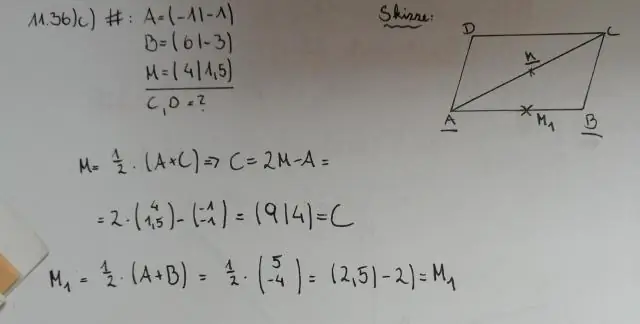
Във всеки паралелограм диагоналите (линиите, свързващи противоположните ъгли) се разделят помежду си. Тоест всеки диагонал разрязва другия на две равни части. На фигурата по-горе плъзнете всеки връх, за да промените формата на успоредника и да убедите себе си, че това е така
За какво се използва квадратен график?
Графика на кутия и мустаци е начин за обобщаване на набор от данни, измерени в интервална скала. Често се използва при анализ на обяснителни данни. Този тип графика се използва за показване на формата на разпределението, неговата централна стойност и неговата променливост